Matrizes - Operações

• Matriz simétrica: matriz quadrada de ordem n tal que A = A^t . Por exemplo,

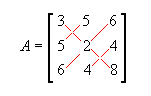é simétrica, pois a₁₂ = a₂₁ = 5, a₁₃ = a₃₁ = 6, a₂₃ = a₃₂ = 4, ou seja, temos sempre       a _ij = a _ij.
   

• Matriz oposta: matriz -A obtida a partir de A trocando-se o sinal de todos os elementos de A. Por exemplo, .

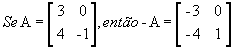Igualdade de matrizes

   Duas matrizes, A e B, do mesmo tipo m x n, são iguais se, e somente se, todos os elementos que ocupam a mesma posição são iguais:

.

• Matriz simétrica: matriz quadrada de ordem n tal que A = A^t . Por exemplo,

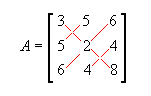é simétrica, pois a₁₂ = a₂₁ = 5, a₁₃ = a₃₁ = 6, a₂₃ = a₃₂ = 4, ou seja, temos sempre       a _ij = a _ij.
   

• Matriz oposta: matriz -A obtida a partir de A trocando-se o sinal de todos os elementos de A. Por exemplo, .

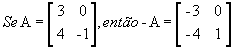Igualdade de matrizes

   Duas matrizes, A e B, do mesmo tipo m x n, são iguais se, e somente se, todos os elementos que ocupam a mesma posição são iguais:

.

 Operações envolvendo matrizes

Adição

   Dadas as matrizes , chamamos de soma dessas matrizes a matriz , tal que C_ij = a_ij + b_ij , para todo :

Exemplos:

Observação: A + B existe se, e somente se, A e B forem do mesmo tipo.

Propriedades

   Sendo A, B e C matrizes do mesmo tipo ( m x n), temos as seguintes propriedades para a adição:

a) comutativa: A + B = B + A

b) associativa: ( A + B) + C = A + ( B + C)

c) elemento neutro: A + 0 = 0 + A = A, sendo 0 a matriz nula m x n

d) elemento oposto: A + ( - A) = (-A) + A = 0

Subtração

   Dadas as matrizes , chamamos de diferença entre essas matrizes a soma de A com a matriz oposta de B:

Observe:

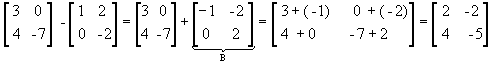
Multiplicação de um número real por uma matriz

   Dados um número real x e uma matriz A do tipo m x n, o produto de x por A é uma matriz B do tipo m x n obtida pela multiplicação de cada elemento de A por x, ou seja, b_ij = xa_ij:

    Observe o seguinte exemplo:

Propriedades

   Sendo A e B matrizes do mesmo tipo ( m x n) e x e y números reais quaisquer, valem as seguintes propriedades:

a) associativa: x . (yA) = (xy) . A

b) distributiva de um número real em relação à adição de matrizes: x . (A + B) = xA + xB

c) distributiva de uma matriz em relação à adição de dois números reais: (x + y) . A = xA + yA

d) elemento neutro : xA = A, para x=1, ou seja, A=A

Adição

   Dadas as matrizes , chamamos de soma dessas matrizes a matriz , tal que C_ij = a_ij + b_ij , para todo :

Exemplos:

Observação: A + B existe se, e somente se, A e B forem do mesmo tipo.

Propriedades

   Sendo A, B e C matrizes do mesmo tipo ( m x n), temos as seguintes propriedades para a adição:

a) comutativa: A + B = B + A

b) associativa: ( A + B) + C = A + ( B + C)

c) elemento neutro: A + 0 = 0 + A = A, sendo 0 a matriz nula m x n

d) elemento oposto: A + ( - A) = (-A) + A = 0

Subtração

   Dadas as matrizes , chamamos de diferença entre essas matrizes a soma de A com a matriz oposta de B:

Observe:

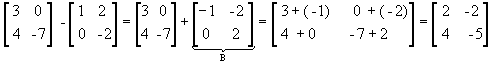
Multiplicação de um número real por uma matriz

   Dados um número real x e uma matriz A do tipo m x n, o produto de x por A é uma matriz B do tipo m x n obtida pela multiplicação de cada elemento de A por x, ou seja, b_ij = xa_ij:

    Observe o seguinte exemplo:

Propriedades

   Sendo A e B matrizes do mesmo tipo ( m x n) e x e y números reais quaisquer, valem as seguintes propriedades:

a) associativa: x . (yA) = (xy) . A

b) distributiva de um número real em relação à adição de matrizes: x . (A + B) = xA + xB

c) distributiva de uma matriz em relação à adição de dois números reais: (x + y) . A = xA + yA

d) elemento neutro : xA = A, para x=1, ou seja, A=A

 ANTERIOR        PRÓXIMA