Denominações especiais
Algumas matrizes, por suas características, recebem denominações especiais.
-
Matriz linha: matriz do tipo 1 x n, ou seja, com uma única linha. Por exemplo, a matriz A =[4 7 -3 1], do tipo 1 x 4.
-
Matriz coluna: matriz do tipo m x 1, ou seja, com uma única coluna. Por exemplo,
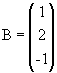, do tipo 3 x 1
-
Matriz quadrada: matriz do tipo n x n, ou seja, com o mesmo número de linhas e colunas; dizemos que a matriz é de ordem n. Por exemplo, a matriz
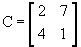é do tipo 2 x 2, isto é, quadrada de ordem 2.
Numa matriz quadrada definimos a diagonal principal e a diagonal secundária. A principal é formada pelos elementos aij tais que i = j. Na secundária, temos i + j = n + 1.
Veja:
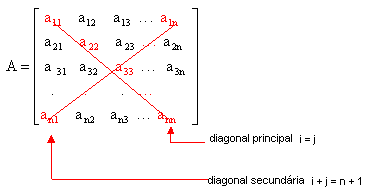
Observe a matriz a seguir:
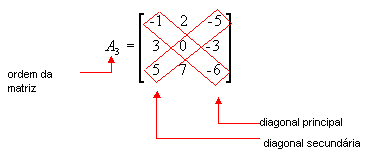
a11 = -1 é elemento da diagonal principal, pois i = j = 1
a31= 5 é elemento da diagonal secundária, pois i + j = n + 1 (3 + 1 = 3 + 1)
-
Matriz nula: matriz em que todos os elementos são nulos; é representada por 0m x n.
Por exemplo, 
.
-
Matriz diagonal: matriz quadrada em que todos os elementos que não estão na diagonal principal são nulos. Por exemplo:
 |
 |
-
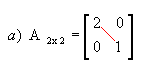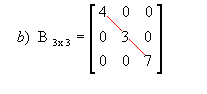Matriz identidade: matriz quadrada em que todos os elementos da diagonal principal são iguais a 1 e os demais são nulos; é representada por In, sendo n a ordem da matriz. Por exemplo:
 |
 |
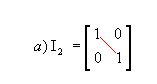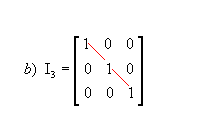Assim, para uma matriz identidade 
.
-
Matriz transposta: matriz At obtida a partir da matriz A trocando-se ordenadamente as linhas por colunas ou as colunas por linhas. Por exemplo:
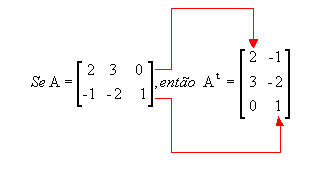
Desse modo, se a matriz A é do tipo m x n, At é do tipo n x m.
Note que a 1ª linha de A corresponde à 1ª coluna de At e a 2ª linha de A corresponde à 2ª coluna de At.