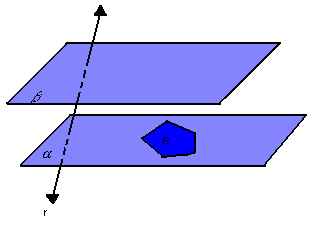
Na figura abaixo, temos dois planos paralelos e distintos, ![]() , um polígono convexo R contido em
, um polígono convexo R contido em ![]() e uma reta r que intercepta
e uma reta r que intercepta ![]() , mas não R:
, mas não R:
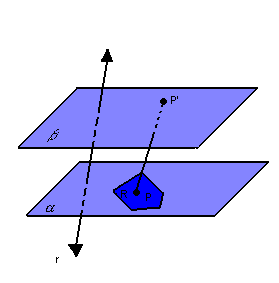
Para cada ponto P da região R, vamos considerar o segmento ![]() , paralelo à reta r
, paralelo à reta r ![]() :
:
Assim, temos:
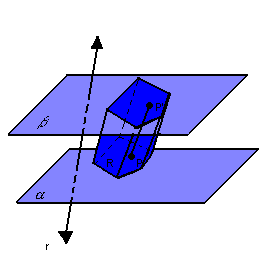
Chamamos de prisma ou prisma limitado o conjunto de todos os segmentos congruentes ![]() paralelos a r.
paralelos a r.
Elementos do prisma
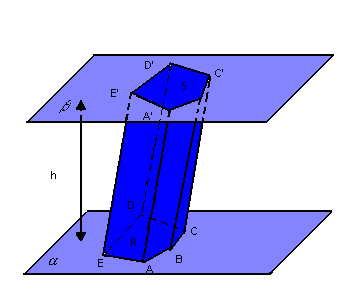
Dados o prisma a seguir, consideramos os seguintes elementos:
-
bases:as regiões poligonais R e S
-
altura:a distância h entre os planos
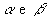
-
arestas das bases:os lados
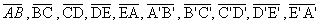 ( dos polígonos)
( dos polígonos) -
arestas laterais:os segmentos
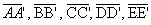
-
faces laterais: os paralelogramos AA'BB', BB'C'C, CC'D'D, DD'E'E, EE'A'A
Classificação
Um prisma pode ser:
-
reto: quando as arestas laterais são perpendiculares aos planos das bases;
-
oblíquo: quando as arestas laterais são oblíquas aos planos das bases.
Veja:
|
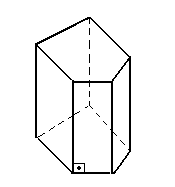
prisma reto |
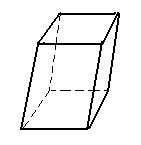
prisma oblíquo |
| Chamamos de prisma regular todo prisma reto cujas bases são polígonos regulares: | |
|
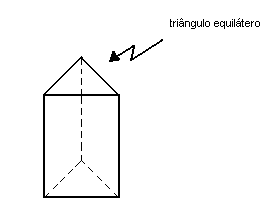
prisma regular triangular |
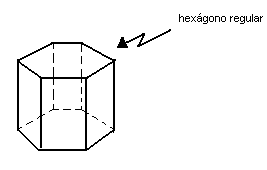
prisma regular hexagonal |
Observação: As faces de um prisma regular são retângulos congruentes.
Secção
Um plano que intercepte todas as arestas de um prisma determina nele uma região chamada secção do prisma.
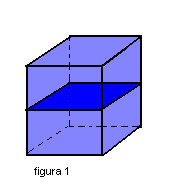
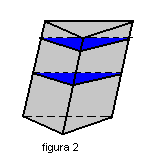
Secção transversal é uma região determinada pela intersecção do prisma com um plano paralelo aos planos das bases ( figura 1). Todas as secções transversais são congruentes ( figura 2).
|
|
|
Áreas
Num prisma, distinguimos dois tipos de superfície:as faces e as bases. Assim, temos de considerar as seguintes áreas:
a) área de uma face (AF ):área de um dos paralelogramos que constituem as faces;
b) área lateral ( AL ):soma das áreas dos paralelogramos que formam as faces do prisma.
No prisma regular, temos:
AL = n . AF (n = número de lados do polígono da base)
c) área da base (AB): área de um dos polígonos das bases;
d) área total ( AT): soma da área lateral com a área das bases
AT = AL + 2AB
Vejamos um exemplo.
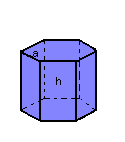
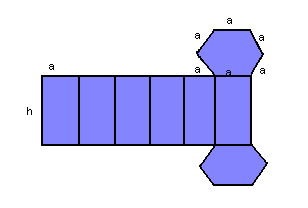
Dado um prisma hexagonal regular de aresta da base a e aresta lateral h, temos:
|
|
|